As an engineer, I absolutely love estimation. Early in high school, I hated it, though. I hated the uncertainty and craved exactitude. By my sophomore year of college, I'd come to appreciate the elegant simplicity of estimation. One of my favorite demonstrations of this elegance is the calculation of Earth's volume.
Just how big is Earth?
Perhaps the best part of estimation is that it can be used to get anything close enough. In elementary and middle school, we were taught to use 3.14 or 22/7 for pi, even though those aren't exact values. For most applications (even beyond grade school math), they're close enough. Ask people what "pi" is. A mathematician will tell you it's the ratio of a circle's circumference to its diameter. A champion pi-digit memorizer will tell you it's 3.14159265... and so on. But an engineer will tell you it's about 3.
How close is that?
With a little estimation (and less knowledge), both questions are easily answered.
According to Wikipedia, the volume of Earth is 1,083,210,000,000 km^3 (or 259,875,899,000 miles^3).
Also according to Wikipedia, the value of pi is 3.14159... to infinity. Also according to Wikipedia, pi has been calculated to around 5,000,000,000,000 digits.
How can we easily calculate Earth's volume?
My favorite way is to use the meter. If you look it up, a meter is defined as the distance light travels, in a vacuum, in 0.00000000333564095 seconds.
While interesting (an precise), this definition is of no use to us. What was the meter originally defined as?
One meter was one ten-millionth of the distance from the North Pole to the Equator. So from the North Pole to the Equator was to measure 10,000,000 meters. We're already estimating. Even though the original definition and the new definition aren't the same, we know the values to be very close (close enough for our purposes).
This is one-fourth of the distance to make a complete circle around the world. This means that the distance around Earth (travelling through both the North and South Poles) is 40,000,000 meters. Here again is an estimation. We know that Earth is not a perfect sphere. For our calculations, though, it is very close.
So now we have Earth's circumference to be 40,000,000 meters. We want to get to volume, so we'll need the radius (or half the diameter). First, we'll use the formula below.
C = 2πr
Circumference equals two times pi times the radius. Plugging in, we get this:
40,000,000 m = 2πr
Simplifying results in:
(20,000,000 m)/π = r
To make things easier, we'll use the fact that 1,000 m = 1 km. This gives us:
(20,000 km)/π = r
We're going to estimate pi to be 3 to see how close we can get.
This gives us:
6,666.6666... km = r
We'll estimate this number a few different ways.
First, we'll try r = 7,000 km.
Second, we'll try r = 6,700 km.
Third, we'll try r = 6,670 km.
Finally, we'll try r = 6,667 km.
How do we calculate volume of a sphere?
We have the following formula:
V = (4/3)(π)(r^3)
Since we're letting pi be 3, the formula simplifies a little.
V = 4(r^3)
So we'll cube our radius in each case.
(1) r^3 = 343,000,000,000 km^3
(2) r^3 = 300,763,000,000 km^3
(3) r^3 = 296,740,963,000 km^3
(4) r^3 = 296,340,742,963 km^3
To find the volume, just multiply each by 4.
(1) V = 1,372,000,000,000 km^3 (or 329,160,305,000 miles^3)
(2) V = 1,203,052,000,000 km^3 (or 288,627,524,000 miles^3)
(3) V = 1,186,963,852,000 km^3 (or 284,767,772,000 miles^3)
(4) V = 1,185,362,971,852 km^3 (or 284,383,700,000 miles^3)
Recall the original volume we found was 1,083,210,000,000 km^3 (or 259,875,899,000 miles^3).
Our estimates were off by between 102,152,971,852 and 288,790,000,000 km^3! That's enormous!
Or is it?
We can find out how "wrong" our guesses are by using the percent error formula.
Using our accepted value from Wikipedia, we obtain the following percent errors:
(1) % Error = 26.66%
(2) % Error = 11.06%
(3) % Error = 9.58%
(4) % Error = 9.43%
Our best estimate was off by less than 9.5%, while our worst was only off by about 27%. What if we'd used a more accurate value for pi? Using 3.14159 gives us radii of 6,000 km, 6,400 km, 6,370 km and 6,366 km. These values result in percent errors of:
(1) % Error = 16.47%
(2) % Error = 1.37%
(3) % Error = 0.05%
(4) % Error = 0.24%
When we used a radius of 6,370 km, we got our best approximation for the volume.
What's Earth's actual radius?
According to Wikipedia, it's 6,371 km, making our radius percent error 0.01%
In the end, our biggest error was letting pi equal three. Even our biggest estimation for the radius gave us a volume off by only about 16.5%. But the less we rounded, the better our guess (when pi was 3).
Is it okay to let pi equal three? Well, sometimes. If a bicycle wheel is two feet wide, the circumference is about 6 feet. In reality, it's closer to 6.28318 feet, but our percent error is 4.5%. In our worst guess about Earth's volume, we were about 74% right. If you want a rough estimate, then by all means use three. If you need a better answer, then use 3.14159.
Anyway, I hope you got something out of this. If not, well, there's always next time.
If you have any questions, or if anything isn't clear, just let me know in the comments.
The image for percent error is from http://www.pstcc.edu.
Most of the information used in my calculation can be found at http://www.wikipedia.org.
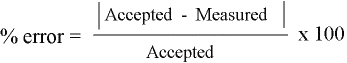
No comments:
Post a Comment