For the purposes of this entry, and infinite root looks like this:
The infinite roots in this entry (like the one above) repeat within themselves. The first one we'll consider is the repeating "root-2." Is there a way to evaluate this? For now, we'll set the repeating infinite root equal to x, the quantity for which we want to solve.
This next part is probably the most important to understand for these problems. If we cover up the biggest square root sign, the first 2 and the first addition sign, what do we see? It's another repeating infinite root. This repeating infinite root is special, because it is exactly what we defined x to be at the beginning.
Using the rule of substitution, we can let everything after that first addition sign be replaced by x. This gives us the far simpler equation below.
In order to solve this problem, we need to get rid of the square root sign. To do that, we square the right-hand sign. Since this is an equation, whatever we do to one side, we must equally do to the other, giving us a new equation.
We now set the left-hand side equal to 0 by subtracting x and 2 from both sides.
Using our rules from Algebra I, we can factor the left-hand side of the equation into (x - 2) and (x + 1). Since we have two things multiplied equal zero, we know one of the two things has to be zero. We then set each factor equal to zero.
On the left problem, we add 2 to both sides. On the right problem, we subtract 1 from both sides. This gives us two answers, 2 and -1.
Let's look at the original repeating infinite root. Notice how no sign is written in front of the root? This means we're looking for a positive root. So now we have to check our answers.
The -1 solution is what is called an extraneous root. This basically means it shows up as an answer from us changing the problem, but it does not solve the original problem. Extraneous roots usually appear whenever you start raising things to powers (e.g. when we squared both sides) or in other cases. We didn't do anything wrong, it's just a part of working with mathematics.
I chose the case with 2 because that's how the problem was introduced to me. My Algebra II/Trig and Math Team Teacher Suzanne Ingram told us that the first time a student saw this, the answer given was 2 because "there were a lot of twos." If you notice, two also was the answer. But is this always the case? Let's look at another example using 3 instead of 2.
Just as before, notice how x is contained under the root after the first 3 and first addition sign.
Now we square both sides.
After subtracting x and 3 from both sides, we notice that this won't factor. I prefer completing the square, but we'll use the quadratic formula since it's faster.
When we work everything out, it simplifies to one plus or minus the square root of thirteen all over two. We separate that out into two solutions, each with a square root of thirteen. The larger is about 2.3 while the smaller is about -1.3.
Notice how one was positive and the other negative? Our original problem did not have a sign, so we want the positive answer. Since the solution that was about -1.3 is negative, we reject it as an extraneous root. This means that our one solution is 1 plus the square root of 13 all over 2 (or about 2.3).
So, yes, it is possible to solve these infinite root problems. Some of them can get quite tricky, but the ones with just one number repeating (with addition) can all be solved like these. And the answer is not always as simple as the number that repeats over and over.
Anyway, I hope you got something out of this. If not, well, there's always next time.
If you have any questions, or if anything isn't clear, just let me know in the comments.
I first saw this problem during my sophomore of high school from my Algebra II/Trig, Precalculus and Math Team teacher Suzanne Ingram.
The images used here were produced by me using Noteshelf for iPad.
The images used here were produced by me using Noteshelf for iPad.










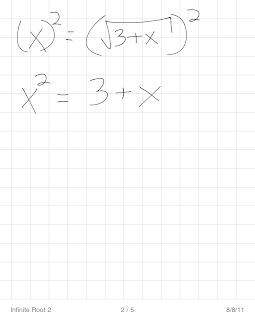
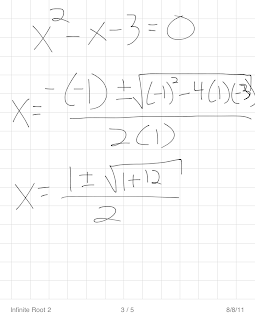


Awesome... Thanks a lot... It helped me... :)
ReplyDeletereally helped me alot
ReplyDeleteSolve this one √4√4-√4√4-....all of them in recursion
ReplyDelete√(6+√(6+√6))=?
ReplyDeleteThere is no infinite root. Now how to solve?
great...................
ReplyDeletereally helped me a lot
great...................
ReplyDeletereally helped me a lot
great...................
ReplyDeletereally helped me a lot
y = √(5+√(5-√(5+....))) !!! find y^2 - y
ReplyDelete2/√5 * 2/(√(2+√5)) * 2/(√(2+√(2+√5))) *...* 2/(√(2+...√5)) = ?
ReplyDeleteHard Rock Hotel & Casino, Reno - Mapyro
ReplyDeleteFind 청주 출장샵 all information and best deals of Hard Rock Hotel & Casino in Reno, 전주 출장마사지 NV. 김포 출장샵 Room 화성 출장안마 Amenities. 24-hour room service. Room Service. 24-hour 양산 출장안마